Logistic Regression
1. Introduction
지난 시간 우리는 Logistic 회귀 알고리즘의 구성과 방법론에 대해 배워보았습니다. 여러분도 알다시피, 로지스틱 회귀분석은 이진 분류를 할 때 사용하는 기법입니다. 다양한 예제를 통해 Logistic Regression을 구현해보도록 하겠습니다. 이번 포스팅은 University Edition을 사용하여 실습을 진행하지만, 코드도 함께 첨부할 테니 BASE 이용자 분들은 코드를 보시면 됩니다.
2. Data
첫 번째 데이터는 1983년에 진행된 Pine씨의 연구입니다. Intra-Abdominal sepsis(복부내 패혈증)를 앓고 있는 환자들에 대해, 수술 후 생존 여부를 예측하기 위해 Logistic 회귀를 사용하였습니다.
<code1>
data Survival;
input ID Status Shock Malnutrition Alcoholism Age BowelInfraction;
datalines;
1 0 0 0 0 56 0
2 0 0 0 0 80 0
3 0 0 0 0 61 0
4 0 0 0 0 26 0
5 0 0 0 0 53 0
6 1 0 1 0 87 0
7 0 0 0 0 21 0
8 1 0 0 1 69 0
9 0 0 0 0 57 0
10 0 0 1 0 76 0
11 1 0 0 1 66 1
12 0 0 0 0 48 0
13 0 0 0 0 18 0
14 0 0 0 0 46 0
15 0 0 1 0 22 0
16 0 0 1 0 33 0
17 0 0 0 0 38 0
18 0 0 0 0 27 0
19 1 1 1 0 60 1
20 0 0 0 0 59 1
21 1 1 0 0 63 1
22 1 1 1 0 70 0
23 1 0 0 1 49 0
24 0 1 0 0 50 0
25 1 1 1 0 70 0
26 1 0 0 1 49 0
27 1 1 0 0 78 1
28 0 0 1 1 60 0
29 0 0 0 1 60 0
30 1 1 0 0 78 1
31 0 0 0 0 28 1
32 0 0 0 0 80 0
33 0 0 0 0 59 1
34 1 0 1 0 50 1
35 1 0 1 0 68 0
36 0 0 0 0 74 1
37 0 0 1 0 27 0
38 1 0 1 1 66 1
39 1 1 1 0 76 0
40 1 0 0 1 70 1
41 0 0 0 0 36 0
42 0 0 0 0 52 1
43 0 0 0 0 30 1
44 1 1 0 1 60 0
45 0 0 1 1 54 0
46 0 0 0 0 65 0
47 1 0 0 0 47 0
48 0 0 1 1 42 0
49 0 0 0 0 22 0
50 0 1 1 0 44 0
;
위 코드를 이용하여 데이터 셋을 생성합니다. University Edition에서 바로 생성해도 되고, SAS BASE를 이용하여 생성 후에 Import해도 됩니다.
3. Table Analysis
먼저 Shock 여부와 생존여부에 대한 빈도를 테이블로 살펴보겠습니다. 좌측의 콘솔에서 다음과 같이 선택합니다.
- 작업▶통계량▶테이블분석
- 데이터▶work.survival
- 역할▶행 변수▶Status, 열 변수▶Shock 추가
<code2>
proc freq data=WORK.SURVIVAL;
tables (Status) *(Shock) / chisq nopercent norow nocol nocum
plots(only)=(freqplot mosaicplot);
run;
BASE 이용자 분들은 위의 코드로 실습을 진행하시면 됩니다.
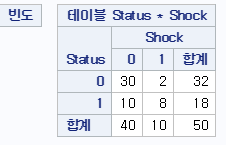
결과를 보니, Shock를 겪었을 경우 사망률은 8/10=0.8, Shock를 겪지 않은 경우 생존율은 10/40=0.25로, Shock를 겪으면 생존율이 상당히 높아지는 것을 알 수 있습니다.
4. Logistic Regression
우리는 지난 시간 오즈비와 Logistic 회귀에 대한 수식을 배웠습니다. 이를 이용하여 통계량에 대한 해석을 진행해보겠습니다. 다음은 우리가 알고자 하는 모형입니다.
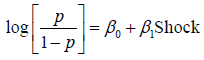
4.1 설명변수 Shock 설정
작업▶선형 모델▶이진 로지스틱 회귀
데이터▶Work.sepsis
역할▶반응 변수▶Status 추가, 관심이벤트▶1 선택
역할▶설명변수▶연속 변수▶ Shock 추가
상단의 “모델” ▶사용자 정의 모델▶편집▶Sock 추가
<code3>
proc logistic data=WORK.SURVIVAL;
model Status(event='1')=Shock / link=logit technique=fisher;
run;
연결함수를 로짓으로 설정했으므로 코드 또한 로짓으로 설정하고, 피셔 검정방법을 사용합니다.
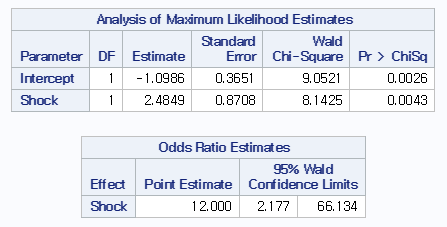
코드 결과를 해석해볼까요? 절편이 -1.10이고, Shock의 계수가 2.48로 계산됩니다. 그러므로 모형은
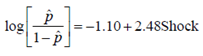
과 같이 구성되고, Shock이 0일 때의 계산은
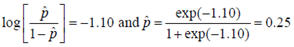
이렇게 되겠죠? 즉, P의 Hat값. 추정값은 0.25고, Survival이 1일 확률 또한 0.25로 추정되는 겁니다.
4.2 Sigmoid 곡선 그리기
작업▶선형 모델▶이진 로지스틱 회귀
데이터▶Work.sepsis
역할▶반응 변수▶Status 추가, 관심이벤트▶1 선택
역할▶설명변수▶연속 변수▶Age 추가
상단의 “모델” ▶사용자 정의 모델▶편집▶Age 추가
상단의 “옵션” ▶도표▶기본 및 추가 도표▶”효과도표” 체크
실행
<code4>
proc logistic data=WORK.SURVIVAL plots=(effect);
model Status(event='1') = Age / link=logit technique=fisher;
run;
<code3>과 다르게 plots 라는 옵션을 추가하시면 됩니다.
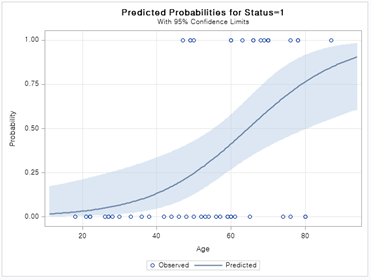
결과를 보면 위와 같은 Sigmoid 곡선이 생성되었습니다. 이를 통해 X 변수에 대한 P추정값을 알 수 있습니다.
5. Conclusion
이번 시간에는 PROC LOGISTIC 코드와, University Edition을 이용하여 로지스틱 회귀 사용법을 익혀보았습니다. 다음시간에는 모든 변수를 할당하여 분석을 진행해 보도록 하겠습니다.
ps. 여러분들이 분석을 할 수 있게 올리는 글인데 코드 복사가 잘 되는지 모르겠네요.
잘 안된다면 댓글 남겨주세요. 또, 원하는 분석기법이 있으시면 말씀해주세요.
'SAS' 카테고리의 다른 글
| [SAS 프로그래밍 실습] Quantile Regression (0) | 2022.01.16 |
|---|---|
| [SAS 프로그래밍 실습] Quantile Regression (0) | 2022.01.16 |
| [SAS 프로그래밍 실습] 로직스틱(LOGISTIC) 회귀를 이용한 PROC PLM 실습 (0) | 2022.01.06 |
| [SAS 프로그래밍 실습] 로직스틱 회귀 분석 [2편](Logistic Regression) (0) | 2022.01.04 |
| [SAS 프로그래밍 실습] Funnel Plot 을 이용한 그룹비교 (0) | 2021.12.07 |




댓글