Quantile Regression
1. Introduction
안녕하세요. 박세훈입니다. 오늘은 회귀분석의 한 종류인 Quantile Regression에 대해 배워보겠습니다. 데이터는 때때로 같은 X값에 여러 개의 Y값을 가진 경우가 있습니다. 본 실습에선 X가 년도이기 때문에 연도별로 여러 개의 Y값을 갖게 되죠. 이럴 때 각 Y값 들의 분포에 따라 다른 모델을 적용하고 합니다. Quantile Regression은 이를 가능케 해줍니다.
2. Data
이 데이터는 미국 통계학 교수 459명의 연도별 급여를 측정한 데이터입니다.
<code1>
data salary;
input Salaries Years @@;
call streaminit(1);
/* for blog example, add random jitter to undo the binning */
Year = years + (rand("테이블",1/3, 1/3) - 2); /* add -1, 0, 1 */
Year = min(Year, 25);
label Salaries='Salaries (1000달러 단위)';
datalines;
54.94 2 58.24 2 58.11 2 52.23 2 52.98 2 57.62 2
44.48 2 57.22 2 54.24 2 54.79 2 56.42 2 61.90 2
63.90 2 64.10 2 47.77 2 54.86 2 49.31 2 53.37 2
51.69 2 53.66 2 58.77 2 56.77 2 53.06 2 54.86 2
50.96 2 56.46 2 51.67 2 49.37 2 56.86 2 49.85 2
50.95 2 56.46 2 48.76 2 55.87 2 60.22 2 50.27 2
56.83 2 56.16 2 54.49 2 57.79 2 52.97 2 54.78 2
56.10 2 55.06 2 56.02 2 56.54 2 54.31 2 63.06 2
52.06 2 51.44 2 52.53 2 58.71 2 58.83 2 57.42 2
56.04 2 51.06 2 49.98 2 56.20 2 51.31 2 48.24 2
54.51 2 54.77 2 51.60 2 54.21 2 52.20 2 55.38 2
51.02 2 51.30 2 50.76 2 54.67 2 53.38 2 54.15 2
52.48 2 56.68 2 57.83 2 56.19 2 49.11 2 60.12 2
50.02 2 67.11 5 68.71 5 62.13 5 64.63 5 61.42 5
68.29 5 62.08 5 67.68 5 66.52 5 73.68 5 60.18 5
49.50 5 60.12 5 69.50 5 48.50 5 61.00 5 54.15 5
51.16 5 48.90 5 68.91 5 62.15 5 52.43 5 59.42 5
60.64 5 51.58 5 70.45 5 62.48 5 68.92 5 59.05 5
59.43 5 61.91 5 66.88 5 60.26 5 54.17 5 69.50 5
70.29 5 60.02 5 61.49 5 50.60 5 65.43 5 65.07 5
67.43 5 68.42 5 63.65 5 56.54 5 73.90 5 62.07 5
63.10 5 59.04 5 59.56 5 72.90 5 73.10 5 62.56 5
62.64 5 66.70 5 73.80 5 64.45 5 63.92 5 71.98 5
55.52 5 58.90 5 58.05 5 65.78 5 70.24 5 55.78 5
54.72 5 57.45 5 64.95 5 57.81 5 55.40 8 53.80 8
74.20 8 67.74 8 54.20 8 65.98 8 64.23 8 65.92 8
61.31 8 62.38 8 63.04 8 65.84 8 60.04 8 65.52 8
64.67 8 64.85 8 64.62 8 66.98 8 69.54 8 67.48 8
62.46 8 64.81 8 68.40 8 63.11 8 58.99 8 68.10 8
68.77 8 65.97 8 67.96 8 64.47 8 65.90 8 59.14 8
65.23 8 73.45 8 64.47 8 58.48 8 60.94 8 58.86 8
69.38 8 66.67 8 62.43 8 63.97 8 69.39 8 65.36 8
74.90 8 64.57 8 75.53 8 70.54 8 73.80 11 53.20 11
66.69 11 54.13 11 59.61 11 75.20 11 53.98 11 78.20 11
59.51 11 68.72 11 51.01 11 76.20 11 61.32 11 58.76 11
60.45 11 67.04 11 61.21 11 66.26 11 53.94 11 61.75 11
59.08 11 64.94 11 75.02 11 65.26 11 56.49 11 72.71 11
55.39 11 62.64 11 62.66 11 66.78 11 63.01 11 61.99 11
65.48 11 58.56 11 60.46 11 58.66 11 62.30 11 61.22 11
61.71 11 71.19 11 59.98 11 68.30 11 56.04 11 64.69 11
52.01 11 58.42 11 58.42 11 56.64 11 65.35 11 56.37 11
63.17 11 63.15 11 59.03 11 61.99 11 51.84 11 56.40 11
60.59 11 71.78 11 60.98 11 65.43 11 69.64 11 57.71 11
57.07 11 60.75 11 69.79 11 65.44 14 76.90 14 77.80 14
71.75 14 65.13 14 69.12 14 64.35 14 61.38 14 64.61 14
61.08 14 66.16 14 76.20 14 69.19 14 75.90 14 52.10 14
64.85 14 53.40 14 66.42 14 58.09 14 54.46 14 69.47 14
60.12 14 65.57 14 60.50 14 63.14 14 59.12 14 59.30 14
65.30 14 55.10 14 54.81 14 66.28 14 65.49 14 68.15 14
55.40 14 58.70 14 75.37 14 58.01 14 57.23 14 63.27 14
64.61 14 61.11 14 62.56 14 67.80 14 56.28 14 56.44 14
59.68 14 59.08 14 62.55 14 64.13 14 61.91 14 63.71 14
60.71 14 65.68 14 59.47 14 65.53 14 75.80 14 75.10 14
59.00 14 63.64 14 64.17 14 70.18 14 67.75 14 63.58 14
72.84 17 73.79 17 73.25 17 68.77 17 77.07 17 74.15 17
68.65 17 58.19 17 57.38 17 60.77 17 60.65 17 60.50 17
74.09 17 61.50 17 77.26 17 60.46 17 55.61 17 69.35 17
59.40 17 71.66 17 74.88 17 59.50 17 58.50 17 69.09 17
59.67 17 63.70 17 76.63 17 75.65 17 78.55 17 68.53 17
75.30 17 69.17 17 77.71 17 62.70 17 58.99 17 59.36 17
74.33 17 71.55 17 56.42 17 68.96 17 68.69 17 76.89 17
74.71 17 69.04 17 72.20 17 70.51 17 69.65 17 54.73 17
70.27 17 69.74 17 72.88 17 79.20 17 62.55 20 59.10 20
72.15 20 58.20 20 57.10 20 75.67 20 60.10 20 66.45 20
68.27 20 57.70 20 68.09 20 77.70 20 72.74 20 64.55 20
66.61 20 64.89 20 67.34 20 69.59 20 70.85 20 70.97 20
74.35 20 77.80 20 78.10 20 66.33 20 77.50 20 76.91 20
68.37 20 72.77 20 70.85 20 70.89 20 74.77 23 83.62 23
69.33 23 82.80 23 57.80 23 59.80 23 67.09 23 60.03 23
67.77 23 68.23 23 66.23 23 71.72 23 81.80 23 60.80 23
63.94 23 81.74 23 73.60 23 77.81 23 60.98 23 65.52 23
60.64 23 69.89 23 72.85 23 77.70 23 61.21 23 74.73 23
58.87 23 58.02 25 68.94 25 85.50 25 53.48 25 61.13 25
63.37 25 83.50 25 85.48 25 56.99 25 75.12 25 57.33 25
85.72 25 64.87 25 51.76 25 51.11 25 51.31 25 78.28 25
57.91 25 86.78 25 58.27 25 56.56 25 76.33 25 61.83 25
69.13 25 63.15 25 66.13 25
3. 모델링
3.1 일반적인 회귀
<code2>
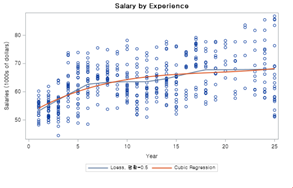
title "경력에 따른 봉급";
proc sgplot data=salary;
loess x=Year y=Salaries / smooth=0.5;
reg x=Year y=Salaries / degree=3 nomarkers legendLabel="Cubic 회귀";
run;
본 데이터에 대해 큐빅 스플라인 회귀를 돌린 결과입니다. 여기선 모수적기법인 GLM대신 비모수적인 Losses를 확인하여 비교해 보았습니다.
3.2 Mean vs Quantile
Quantile과 mean을 비교하기 위해, mean과 Quantile별 mean을 계산합니다.
<code2>
proc means data=salary noprint;
class year;
var salaries;
output out=outP(where=(_TYPE_>0)) Mean=Mean Q1=Q1 Median=Median Q3=Q3;
run;
data All; /*평균과 분위 별 평균 데이터를 저장합니다. */
merge salary outP;
by year;
run;
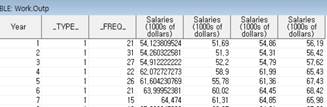
Quantile별로 평균 데이터 값들을 연결합니다.
<code3>
title "Connect the Dots: Quantiles of Salary for Each Year";
proc sgplot data=All;
scatter x=Year y=Salaries / transparency=0.5;
series x=Year y=Q1 / curvelabel="Q1";
series x=Year y=Median / curvelabel="Q2";
series x=Year y=Q3 / curvelabel="Q3";
run;
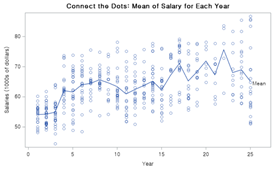
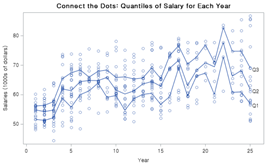
<좌측> 전체 데이터 평균 / <우측> 분위 별 데이터 평균
3.3 Quantile Regression
<code4>
title "Quantile Regression of Salary vs. Year";
ods graphics on;
proc quantreg data=salary ci=sparsity;
model salaries = year year*year year*year*year / /*X+X^2+X^3로 모델링*/
quantile=0.25 0.5 0.75 plot=fitplot(showlimits);
run;
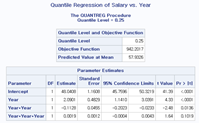
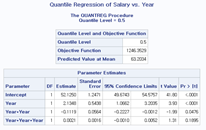
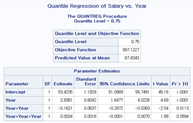
Quantreg 프록시져를 사용하여 분위 별로 회귀 계수들과 p값을 확인할 수 있습니다. 이렇게 하게 되면 수입이 높은 그룹, 낮은 그룹 등으로 나눠서 회귀분석을 해볼 수 있으며, 그룹간의 편차와 특성이 심한 데이터에 적용하면 유용합니다. 아래 결과를 보면, 표준적인 회귀방법을 적용함에 따라 그룹별 회귀 적합이 크게 다르지 않군요.
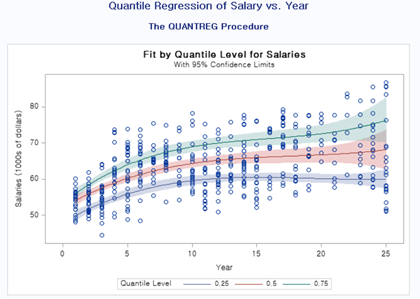
3.4 Quantile Regression (비 모수적 기법)
분위 별로 적합을 더 유용하게 하기 위해, 비 모수적 기법을 사용해 보겠습니다.
title "Nonparametric Quantile Regression (연도를 독립 변수로 설정)";
proc quantreg data=salary;
effect sp = spline(year); /*year를 독립변수 평활화 후 모델링*/
model salaries = sp /quantile=0.25 0.5 0.75 plot=fitplot;
run;
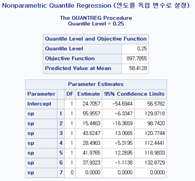
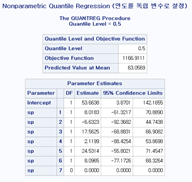
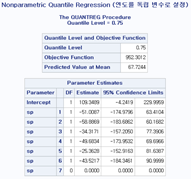
마찬가지로 Qunatreg 프록시져를 사용하고, 비모수적인 방법을 사용하기 위해 spline함수를 year에 적용해주었습니다. 마찬가지로 각 분위 별 계수와 추정치들을 확인할 수 있습니다.
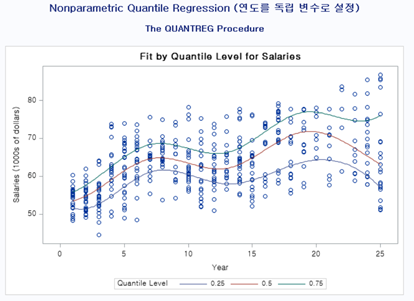
재밌는 결과를 확인할 수가 있네요. 첫 연봉은 크게 차이가 없지만, 나중에 갈수록 3분위에 해당하는 교수들이 훨씬 많은 봉급을 받는다는 것을 알 수가 있었습니다.
4. Conclusion
현실에서 그룹은 굉장히 많은 의미를 담고 있습니다. 그것이 금융 데이터이건, 체력 데이터이건, 그룹이란 분할은 아주 유용하게 분석될 수 있습니다. 이러한 기법을 알아둔다면 실제 데이터에 모델을 적용할 수 있는 역량이 늘어날 것입니다.
'SAS' 카테고리의 다른 글
| [SAS 프로그래밍 실습] 가중 회귀 분석(Weight Regression) 구현하기 (0) | 2022.01.19 |
|---|---|
| [SAS 프로그래밍 실습] Histogram Overlay (0) | 2022.01.17 |
| [SAS 프로그래밍 실습] Quantile Regression (0) | 2022.01.16 |
| [SAS 프로그래밍 실습] 로직스틱(LOGISTIC) 회귀를 이용한 PROC PLM 실습 (0) | 2022.01.06 |
| [SAS 프로그래밍 실습] 로직스틱 회귀 분석 [2편](Logistic Regression) (0) | 2022.01.04 |




댓글