Monte Carlo Estimate
1. Introduction
안녕하세요 박세훈입니다. 몬테카를로 알고리즘에 대해서 들어 보신적 있나요? 흔히 확률적 기법이라고도 불리는 위 알고리즘은, 대용량 데이터에서 낮은 정확도지만 빠른 성능을 보이는 알고리즘입니다. 자세한 이론은 향후 “SAS 고수의 팁”란에 추가로 포스팅하겠습니다.
예를 들어 100억개의 신용카드 트랜잭션 데이터의 중앙값을 찾아보도록 하죠. 전통적인 방식의 PROC MEAN을 사용하면 굉장히 오랜 시간이 걸립니다. 하지만 사실 중앙값이 16.45$든, 16.5$든 중요하지 않죠. 근사값만 구하면 되니까요. 이럴 때 사용되는 것이 몬테카를로 기법입니다.
2. Data
학습속도와 성능 차이를 비교하기 위해, 10000000(천 만개) 개의 무작위 데이터를 생성하도록 하겠습니다. 데이터의 무작위 성을 더하기 위해, 지수분포와 정규분포를 혼합한 데이터를 생성하겠습니다.
<code1>
%let N = 1e7;
data Have;
call streaminit(12345);
do i = 1 to &N;
d = rand("Bernoulli", 0.6);
if d = 0 then
x = rand("Exponential", 0.5);
else
x = rand("Normal", 10, 2);
output;
end;
keep x;
run;
데이터 분포는 다음과 같습니다.
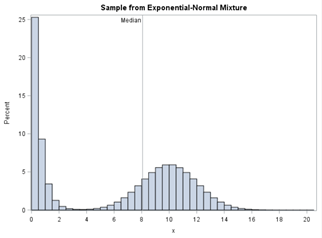
지수분포와 정규분포가 혼합되어 중앙값을 예측하기 어려운 형태가 되었습니다.
3. 중앙값 계산
3.1 Traditional Method
전통적 방식인 PROC MEANS를 사용해보겠습니다.
<code2>
proc means data=Have N Median;
var x;
run;
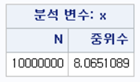
실행시간은 6.36초, PROC MEANS에 의한 계산 결과는 아주 정확하겠죠.
3.2 Naive Resampling
천 만개의 데이터를 직접 계산하는 것은 부하가 심하니, 10%를 추출하여 전통적인 기법으로 중앙값을 계산해 보겠습니다.
<code3>
proc surveyselect data=Have seed=1234567 NOPRINT
out=SubSample
method=urs samprate=0.1; /* 10% 샘플링 */
run;
title "Estimate from 10% of the data";
proc means data=SubSample N Median;
freq NumberHits;
var x;
run;

실행시간은 0.48초, 실제 중앙값인 8.065와도 큰 차이가 없네요.
3.3 Monte-Carlo 기법
Monte Carlo기법으로 Median값을 찾는 과정은 다음과 같습니다.
1. N개의 데이터에서 ¾복원 추출을 한 K개의 표본을 선택합니다.
2. 이렇게 K개의 사이즈로 Resampling된 데이터를 R이라고 정의합니다.
3. 원본데이터의 Median값을 포함하는 Lower, Upper Sentinel을 정의합니다.
<code4>
proc iml;
/* Choose a set R of k = N##(3/4) elements in x, chosen at random with replacement.
Choose quantiles of R to form an interval [L,U].
Return the median of data that are within [L,U]. */
start MedianRand(x);
N = nrow(x);
k = ceil(N##0.75); /* 샘플 추출*/
R = T(sample(x, k)); /* 부트 스트랩 샘플링*/
call sort(R); /* 데이터 정렬 */
L = R[ floor(k/2 - sqrt(N)) ]; /* 하위 sentinel */
U = R[ ceil(k/2 + sqrt(N)) ]; /* 상위 sentinel */
UTail = (x > L); /* 큰 값에 대한 Indicator*/
LTail = (x < U); /* 작은 값에 대한 Indicator */
if sum(UTail) > N/2 & sum(LTail) > N/2 then do;
C = x[loc(UTail & LTail)]; /* extract central portion of data */
return ( median(C) );
end;
else do;
print "Median not between sentinels!";
return (.);
end;
finish;
/* run the algorithm on example data */
use Have; read all var {"x"}; close;
call randseed(456);
t1 = time();
approxMed = MedianRand(x); /* 확률적 중앙값 추정 */
tApproxMed = time()-t1;
t0 = time();
med = median(x); /* 전통적 중앙값 추정*/
tMedian = time()-t0;
results = (approxMed || med) // (tApproxMed|| tMedian);
print results[colname={"Approx" "Traditional"}
rowname={"Estimate" "Time"} F=Best6.]; /* 소수점 자릿수 설정*/
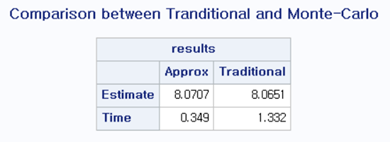
결과로 산출된 테이블입니다. Approx의 경우 Monte – Carlo방식이고, Traditional의 경우 전통적 방법으로 산출된 값입니다. 각각 8.071, 8.065로 매우 유사하게 측정되었습니다. 반면 Apporx의 경우 시간이 0.35로, 전통적 방법에 비해 4배 정도 빠른 속도를 보입니다.
위와 같은 상황에서, 근사값만 구해도 된다면 확률적 접근법이 매우 효율적으로 판단됩니다.
4. Conclusion
때때로 우리는 성능보다 속도를 중요시할 때가 있습니다. 이러한 스킬들을 많이 알아 둔다면, 시의적절한 분석을 통해 효율적으로 데이터를 다루는 데이터 사이언티스트가 될 수 있다고 생각합니다.
'SAS' 카테고리의 다른 글
| [SAS 프로그래밍 실습] IML로 Kernel Regression 구현하기 (0) | 2022.08.10 |
|---|---|
| [SAS 프로그래밍 실습] Restricted Cubic Regression (0) | 2022.08.09 |
| [SAS 프로그래밍 실습] 가중 회귀 분석(Weight Regression) 구현하기 (0) | 2022.01.19 |
| [SAS 프로그래밍 실습] Histogram Overlay (0) | 2022.01.17 |
| [SAS 프로그래밍 실습] Quantile Regression (0) | 2022.01.16 |




댓글