Kernel Regression
1. Introduction
지난 시간 우리는 Kernel 회귀 알고리즘의 구성과 방법론에 대해 배워보았습니다. 여러분도 알다시피, 커널 회귀는 데이터 간의 심플한 선형 관계가 없을 때 사용되는 기법입니다. 오늘은 연료/산소 비율에 따른 질소산화물(대기 오염에 기여하는) 데이터로 Kernel Regression을 구현해보도록 하겠습니다.
2. Data
<code1>
data gas;
label NOx = "Nitric oxide and nitrogen dioxide";
label E = "Air/Fuel Ratio";
input NOx E @@;
datalines;
4.818 0.831 2.849 1.045 3.275 1.021 4.691 0.97 4.255 0.825
5.064 0.891 2.118 0.71 4.602 0.801 2.286 1.074 0.97 1.148
3.965 1 5.344 0.928 3.834 0.767 1.99 0.701 5.199 0.807
5.283 0.902 3.752 0.997 0.537 1.224 1.64 1.089 5.055 0.973
4.937 0.98 1.561 0.665
;
run;
위 코드를 이용하여 데이터를 불러와 줍니다. 데이터는 종속변수와 설명변수 두 가지로 구성되어 있습니다. Label은 변수에 이름을 붙여주는 기능이 있습니다. 코드 상의 편의를 챙기면서 위와 같이 긴 이름을 출력할 때 용이합니다.
3. Implementation
커널 회귀의 구현 과정은 다음과 같습니다.
3.1 커널 형태와 Bandwidth(Smoothing) Parameter를 정합니다.
커널 밀도 함수를 정하는 것은 크게 중요하지 않습니다. 이 실습에서 저희는 정규 밀도 함수를 커널로 사용합니다. 중요한 것은 Bandwidth(=h)를 정하는 것인데, 전 포스팅에서 언급한 것처럼 큰 Bandwidth를 설정할 경우 Underfit이 되고, 너무 작은 Bandwidth는 과적합 된 모델을 제작합니다.
3.2 근접한 데이터 가중치 설정
확률 밀도 함수를 사용하여 쉽게 가중치를 구할 수 있습니다. SAS/IML에서 데이터 값의 벡터를 PDF에 넣으면 모든 가중치를 한 번에 구할 수 있습니다.
3.3 회귀 계산
위 예측 모형에서, x0에 의한 추정치 ŷ0 는 ‘해당 구간에 할당된‘가중치를 적용한 회귀 추정값입니다. 즉, Bandwidth값에 따라 계수를 추정하는 구간이 나눠질 것이고, 구간 별로 산출된 회귀계수를 적용시키는 것입니다. 구간의 개수가 n->∞ 일수록 곡선이 부드러워집니다.
<code2>
proc iml;
/* 코드에 앞서, 우리는 이전 Weighted regression 시간에 PolyRegEst 모듈을 생성했습니다. 자세한 내용은
https://blog.naver.com/statpark1014/221530810392
를 참고하시기 바랍니다.
*/
/* 대역폭 h의 식은 h=H*range(X)입니다. H는 Proportion of range로, x의 범위를 쪼개주는 역할을 합니다.
X0의 가중치는 N(x0, h)인 분포의 확률밀도 함수 f(x; x0,h)에 의해 계산됩니다.
즉 이는 표준정규분포에 대한 (1/h)*pdf("Normal", (X-x0)/h) 과 같습니다. */
start GetKernelWeights(X, x0, H);
return pdf("Normal", X, x0, H*range(X));
/* bandwidth(대역폭)h = H*range(X) */
finish;
start KernelRegression(X, Y, H, _t=X, deg=1);
t = colvec(_t);
pred = j(nrow(t), 1, .);
do i = 1 to nrow(t);
/* Kernel regression 모듈을 작성합니다.
t is a vector of values at which to evaluate the fit. By default t=X.
*/
/* 자유도 deg 하에서 커널에 대한 확률밀도함수를 계산합니다. */
W = GetKernelWeights(X, t[i], H);
b = PolyRegEst(Y, X, W, deg);
pred[i] = PolyRegScore(t[i], b); /* PolyRegScore 모듈 또한 Weighted regression 포스팅에서 제작 하였습니다. 바로 위 줄에서 회귀계수 b 가 산출되었고, 이를 통해 예측값 행렬 Pred[i]를 생성하였습니다 */
end;
return pred;
finish;
이제 계산을 위한 모든 함수 모듈 생성을 마쳤습니다. 이제 데이터를 불러오고, H 파라미터나 자유도 등을 조정하며 분석을 진행하겠습니다.
<code3>
use gas; read all var {E NOx} into Z; close;
call sort(Z); /* 임시 Z를 만들어 X,Y값을 정렬합니다.*/
X = Z[,1]; Y = Z[,2];
H = 0.1; /* 대역폭 계산을 위한 H값을 정해줍니다. H값에 따라 모델 적합이 달라집니다. */
deg = 1; /* 자유도*/
Npts = 201; /* number of points to evaluate smoother */
t = T( do(min(X), max(X), (max(X)-min(X))/(Npts-1)) ); /* Uniform Grid 생성 */
pred = KernelRegression(X, Y, H, t); /* 예측값 데이터 생성 */
Z=t||pred;
create RegFit from Z[c={"t" "pred"}];
append from Z;
quit;
IML을 종료합니다. 이제 모델을 적합하여 그래프를 생성해보겠습니다.
4. Visualization
<code4>
data RegAll; /*모델 평가를 위한 데이터셋을 생성합니다*/
LABEL pred = 'Kernel model';
merge gas regfit; /*실제 데이터와 추정값 결합*/
run;
title1 'Kernel Estimator ';
title2 'h=0.1*Range(x)';
proc sgplot data=RegAll;
scatter x=E y=NOx / filledoutlinedmarkers markerattrs=(size=6 symbol=CircleFilled);
series x=t y=Pred / curvelabel;
xaxis grid; yaxis grid;
run;
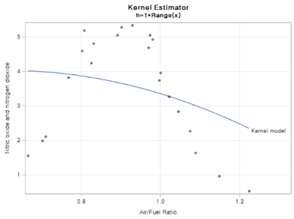
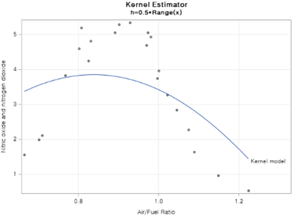
H를 각각 1, 0.5로 지정한 그래프입니다. 아직 까진 적합이 제대로 되지 않습니다.
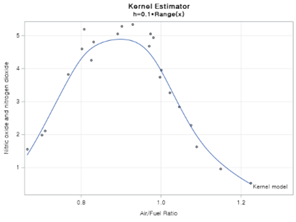
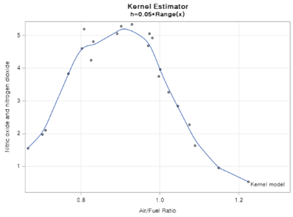
H가 0.1일때 아주 좋은 모델이 적합됩니다. 0.05로 하니까 못생긴 과적합 모델이 나왔군요.
저는 일반화된 모형을 위해 H=0.1인 Kernel을 채택하도록 하겠습니다.
이상으로 Kernel 회귀를 구현하는 것까지 전부 완료하였습니다. 조금은 어려운 내용이었지만, IML을 통해 원론적으로 회귀모형에 접근하는 좋은 경험을 할 수 있었습니다.
5. Appendix
심화 학습을 위해서, Naradya-Watson 커널 모듈을 첨부하겠습니다. 모델 구현을 해보고 싶으신 분들은 밑의 모듈을 참고하여 구현해보시기 바랍니다.
proc iml;
/* Nadaraya-Watson 커널 추정기는 지역 가중 평균을 가중치에 적용하는 기법입니다.
자세한 내용은
https://blog.naver.com/statpark1014/221500082987
을 참고하시기 바랍니다.*/
start NWKerReg(Y, X, x0, H);
K = colvec( pdf("Normal", X, x0, H*range(X)) );
return( K`*Y / sum(K) );
finish;
start NWKernelSmoother(X, Y, H, _t=X);
t = colvec(_t);
pred = j(nrow(t), 1, .);
do i = 1 to nrow(t);
pred[i] = NWKerReg(Y, X, t[i], H);
end;
return pred;
finish;
quit;
6. Restriction
이러한 커널 회귀에도 여러가지 단점이 있습니다. 대역폭이 너무 작으면 모델 구현이 불가능합니다. (Ex 0.001 같은 대역폭은 계산할 수 없음. ) 만약, h가 d/10보다 작으면 midpoint를 예측할 방법이 없습니다. (ex {x[i+1]+x[i]}/2) 이 경우엔 가중치가 0으로 계산됩니다. 이 경우 로스 회귀가 그 대안이 될 수 있는데, 로스 회귀는 가까운 이웃을 사용하므로 이러한 단점을 극복할 수 있습니다.
'SAS' 카테고리의 다른 글
| [SAS 프로그래밍 실습] Restricted Cubic Regression (0) | 2022.08.09 |
|---|---|
| [SAS 프로그래밍 실습] Monte-Carlo Estimate (0) | 2022.01.20 |
| [SAS 프로그래밍 실습] 가중 회귀 분석(Weight Regression) 구현하기 (0) | 2022.01.19 |
| [SAS 프로그래밍 실습] Histogram Overlay (0) | 2022.01.17 |
| [SAS 프로그래밍 실습] Quantile Regression (0) | 2022.01.16 |




댓글