안녕하세요 파키노 랩입니다.
이번시간에는 종속변수가 이진 반응 변수로 분류되는 경우에 사용할 수 있는 회귀 기법인 로지스틱 회귀 분석(Logistic Regression)에 대해 배워 보겠습니다.
1. Instroduction
예를 들어, 여러분이 어떤 질병을 연구하고 있을 때 수술 후 사망일지 생존일지를 통계적으로 분석하고 싶습니다. 그렇기 위해선 생존에 대한 반응 변수가 0과 1사이의 확률로 표현이 되어야 하는데 일반적인 회귀 분석의 경우 그렇지 않죠. 그렇기 때문에 반응 변수를 0과 1사이의 확률값으로 나타낸 회귀를 로지스틱 회귀 분석이라고 합니다.
2. Configuration
로지스틱 회귀분석에 중요한 요소는 크게 세 가지가 있습니다. 하나는 “Odds”라고 불리는 파라미터와, 이를 이용한 "로짓 변환" 그리고 출력값을 뱉어내는 "시그모이드 함수"가 있습니다.
2.1 Odds
오즈는 수리통계학에서 흔히 사용되는 개념으로 승산이라고 부르기도 합니다. 식을 보면 “p/(1 − p)” (p는 확률일 때) 로 구성되어 있는데요, 쉽게 말해서 사건이 일어나지 않을 확률 대비 사건이 일어날 확률를 말합니다. P는 확률이므로, 오즈의 범위는 [0, ∞]이 됩니다. 만약 동전 던지기처럼 두 확률이 동일한 경우 오즈는 1이 되고, 승산은 작지도 크지도 않은 평형을 이루게 됩니다. 만약 p=0.8인 사건이 있다면, Odds는 4가 되고, 사건이 일어날 확률이 4배의 승산이 있다는 것을 알 수가 있습니다.
2.2 Logit
Odds에 대한 이해가 되셨다면, 이제 Logit을 보겠습니다. 로지스틱 회귀 분석의 식을 살펴보면,
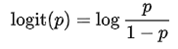
,
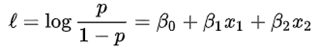
로 구성되어 있습니다. 일반적인 회귀모형과 비교하면 Y대신 log(p/1-p)로 되어 있는 것을 알 수 있습니다. 즉 LOG(Odds)가 로지스틱 회귀의 반응변수가 되는 거죠. 그 이유는 이항 확률의 Odds 범위가 [0, ∞]인 것을 회귀분석과 동일한 [-∞, +∞] 로 변환하기 위해서고, 위의 식을 “로짓 변환”이라고 부릅니다.
2.3 시그모이드 함수
위 로짓 모형의 P값은 우리가 알고 싶은 값입니다. 즉, 어떤 사건이 발생할 추정 확률을 구하면 사건이 발생할지, 아니면 발생하지 않을 지 예측할 수 있기 때문이죠. 로짓 모형을 정리하면,,,
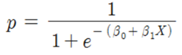
이처럼 P에 대하여 로짓 모형을 정리한 함수를 시그모이드 함수라고 합니다. 모든 추정값을 [0,1]사이의 확률값으로 바꿔주는 역할을 하죠. 시그모이드의 형태는 다음과 같습니다.
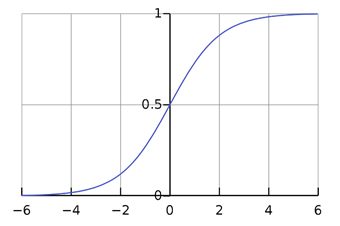
즉 X의 어떤 값을 넣으면, 그 X가 1에 해당할지, 0에 해당할지에 대한 확률값을 뱉는 함수입니다.
3. Prove
유도를 통해 어떻게 함수가 생성되었는지 증명해보겠습니다.
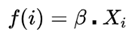
위는 저희가 흔하게 보는 선형 예측 변수입니다.
이제 이를 가지고 시그모이드 함수까지 만들어보겠습니다.
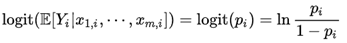
우선, 입력값 p의 범위가 [0,1]일 때 (즉, 기본 데이터로부터 산출된 0과 1사이의 확률값) 출력값의 범위가 [-∞, +∞]로 되도록 로짓 변환을 해줍니다.
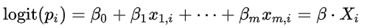
로짓 변환의 결과는 X에 대한 선형함수와 동일하므로, 위의 두 식을 결합하면
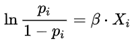
가 됩니다.

그리고 위와 같이 간단하게 정리하면 시그모이드 함수가 되었습니다.
이를 종합하면, Pi는 우리가 구하고자 하는 특정 독립변수 x에서, 종속변수인 “사건이 일어날 확률”을 구하는 것이죠.
4. 모델 적합
모델 적합은 최대가능도 법을 이용해서 진행합니다. Likelihood를 통해 추정을 진행하는데, 이 부분의 경우는 차후 최대가능도 법 MLE를 포스팅 한 후 자세히 다루도록 하겠습니다. 또한 검증을 할 때 가능도비 검정을 통해 카이제곱분포와 근사함으로서 편차를 검정하는데, 이 또한 추후 자세히 다루도록 하겠습니다.
다음시간에는 로지스틱 회귀를 통해 실습을 진행하겠습니다.
'통계학' 카테고리의 다른 글
| [데이터 분석] 어떤 분석 모델을 사용해야 할까? (Machine Learning 모델 기법 정리) (0) | 2022.01.05 |
|---|---|
| [데이터 분석] Weighted Linear Regression- 가중 선형 회귀 (Weighted Least Square) (1) | 2021.12.16 |
| [데이터 분석] Kernel Regression- 커널 회귀 (1) | 2021.12.06 |
| [데이터 분석] Funnel Plot - 깔때기 도표 (0) | 2021.12.05 |
| [회귀 분석] 단순 회귀 모형 추정, 방정식 유도 (1) | 2021.11.28 |




댓글