본 포스팅은 회귀분석의 선수 지식이 요구되는 내용을 포함하고있습니다.
Weighted linear Regression _이론 [weighted least square].
1. introduction.
여러분들도 아시다시피, 선형회귀 분석은 등분산성 가정을 기반으로 분석이 진행됩니다. 그런데 만약 등분산성이 만족하지 않는다면 어떻게 해야 될까요?. 혹은 데이터를 조정한다고 해도, 모든 데이터를 등분산성에 만족시킬 수 있을까요? 여기서 고안된 방법이 바로 가중 선형 회귀, 일명 가중 최소 제곱법입니다.
2. Assessment
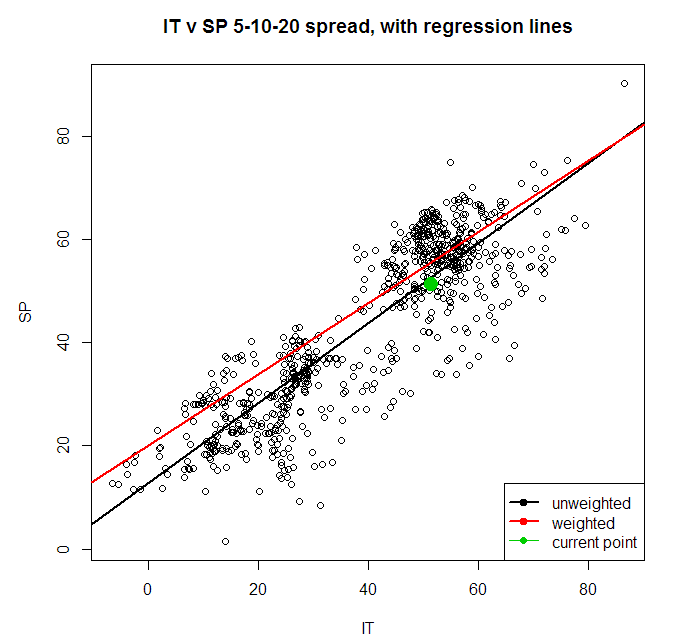
가중회귀는 일반 선형회귀보다 조금 더 "유연하다"라고 말할 수 있습니다. 가중 최소제곱법 이라고 불리는 이 기법은, 편차를 이용한 최소제곱법에 기반하지만 조금 더 발전한 형태를 띄고 있습니다.
기존 최소제곱법이 잔차의 제곱을 최소로하는 거였다면, 본 기법은 잔차에 가중치를 적용한 제곱 값을 최소로 하는 기법입니다. 때문에 가중치를 어떻게 적용하냐에 따라 결과가 다양해 질 수 있습니다. 그렇다고 해서 가중 최소제곱법이 일반 (비가중) 최소제곱법보다 좋다고는 말할 수 없습니다. 하지만, 특별히 이런 모델이 고안된 이유는 어떠한 상황에서 weighted 된 제곱법이 더 정확하기 때문입니다.
예를 들어, 기존의 선형회귀분석은 등분산성을 가정하고 진행하게됩니다. 오차항의 분산이 일정하다는 것은 그만치의 오차를 예측하는데 있어 좀 더 정확한 오차를 계산할 수 있으니까요. 그런데 등분산성이 성립하지 않는 경우 , 즉 어떠한 오차의 분산은 크고, 어떠한 오차항의 분산은 작다면 여기에 가중치를 적용하여 등분산성을 맞춰주는 것입니다. .
주의해야 할 점은 빈도와 가중치는 비슷하면서도 다르다는 겁니다. 어떠한 측정값의 빈도가 많다고 해서 그 값이 더 큰 신뢰를 준다고 생각하면 이 또한 가중치가 되겠지만, 여기서 말하는 가중치는 오차항에 대한 가중치를 말하는 것입니다.
3. Methodology
우선 선형회귀와의 비교를 위해, 수식을 비교하는 식으로 개괄하겠습니다.

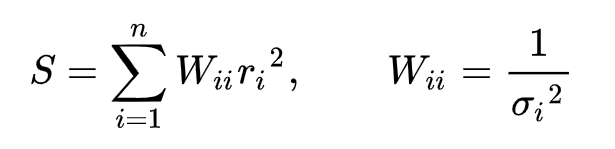
흥미롭게도, 가중치는 해당 관측치의 분산의 역수입니다. 등분산성이 성립되지 않으므로 잔차의 분산이 다를테고, 이것이 잔차에 적용되어 조정 파라미터 역할을 하게 됩니다. 분산이 큰 잔차는 잔차제곱합을 결정하는데 많은 역할 을 하지 못하겠군요. 반면 분산이 작은 잔차는 잔차제곱합을 결정하는데 많은 기여를 할 것으로 보입니다.

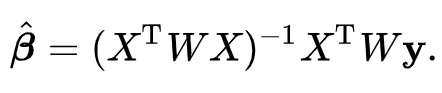
가중 회귀선형 분석을 정리해보면, 어떤 가중치가 크다는 것 - 해당 가중치가 제곱합에 많은 기여를 한다 - 분산이 작은 관측치는 신뢰할 수 있다 - 분산이 큰 관측치는 신뢰하기 어렵다. 라는 결론을 내릴 수 있습니다.


예를 통해 좀 더 쉽게 이해해볼까요?
어떤 과학자가 실험을 하고 있는데, X=13 혹은 14라는 값을 세 번 실험하면 결과값이 1.5 , 3.5 , 4.5 등의 결과가 나오고, X=10혹은을 넣을때 2.9, 3.0, 3.3 등의 결과가 나옵니다. 어떤 X값이 더 신뢰가 있을까요? 분산이 작은 X=10이 더 큰 신뢰도를 갖겠죠? 과학자는 이 실험을 회귀분석으로 결과를 내고 싶은데, X=10 일때의 설명력을 다르게 적용하고 싶습니다.
이 때 사용하는 것이 "가중 선형회귀 분석"이 되는 겁니다.
그래프를 통해 예를 들어 봅시다.
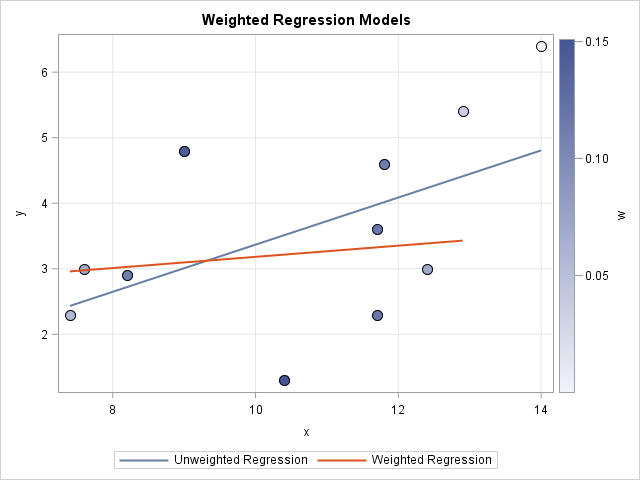
빨간선 = 가중 회귀 / 파란선 = 일반 회귀
X가 13, 14로 갈 수록 관측치의 신뢰가 떨어집니다. ( 즉 관측치의 분산이 크다는 것)
X는 10에서 매우 높은 수준의 신뢰를 가집니다. ( 즉, X=10일 때 일정한 결과만 나온다는 것)
여기서 X=10일 때 높은 가중치를 갖게 되고, X=14일 때 낮은 가중치를 갖게됩니다.
그러므로 가중회귀 곡선은 x=13,14의 관측치에 영향을 덜 받게 되어 낮은 기울기를 갖게 됩니다.
4. Restriction
가중회귀는 일일이 관측치 X값에 따른 가중치를 계산하고, 다시 가중치를 적용한 회귀식을 산출해야하므로 많은 양의 연산이 필요합니다. 컴퓨팅 사양이 증가되면 해결될 일이겠지만, 아직도 실무데이터의 방대한 양을 처리하기엔 다소 어려움이 있어보입니다. ROI를 잘 생각하여 일반 회귀로도 충분히 유의미한 결과를 얻을 수 있는지 분석가의 판단이 필요합니다.
이해가 잘 되셨나요? 다음시간에는 SAS를 통해 가중회귀 실습을 진행하도록 하겠습니다.
질문은 댓글이나 쪽지 부탁드립니다 ^_^
'통계학' 카테고리의 다른 글
| [데이터 분석] 어떤 분석 모델을 사용해야 할까? (Machine Learning 모델 기법 정리) (0) | 2022.01.05 |
|---|---|
| [데이터 분석] Logistic Regression- 로지스틱 회귀 분석 (0) | 2021.12.15 |
| [데이터 분석] Kernel Regression- 커널 회귀 (1) | 2021.12.06 |
| [데이터 분석] Funnel Plot - 깔때기 도표 (0) | 2021.12.05 |
| [회귀 분석] 단순 회귀 모형 추정, 방정식 유도 (1) | 2021.11.28 |




댓글