본 포스팅은 회귀분석의 선수 지식이 요구되는 내용을 포함하고있습니다.
Kernel Regression _이론.
1. introduction.
여러분들도 아시는 것처럼, 선형 회귀분석은 통계분석에서 아주 중요한 기법으로 평가되어 왔습니다. 그럼에도 ‘선형’이라는 한계로, 불규칙적 데이터 예측을 위한 여러가지 파생 모델들이 발전해 왔습니다. 오늘은 그 중에 ‘Kernel Regression’을 배워보겠습니다. 기존 회귀분석의 선형 적합의 단점으로 인해, 좀 더 복잡한 데이터를 해석하려 고안된 모델입니다.
2. Assessment

커널 회귀는 기존의 비선형 데이터에 적합할 수 있다는 점에서 선형 회귀와 가장 큰 차이를 보입니다. 특히, 선형 회귀분석은 데이터가 정규성을 띈다는 가정하에 모수 추정 기법으로 분류되는 반면, 커널 회귀는 이러한 정규성 가정을 하지 않음으로써 “비모수 추정 기법” 으로 분류됩니다. 이는 언뜻 비슷해 보이는 다항 회귀와 커널 회귀에 명확한 차이점을 보여줍니다.
3. Methodology
커널 회귀 분석에는 대표적으로 3가지 방법론이 있습니다. 세 개의 식 전부 선형회귀식에 모태를 두고 있으며, KDE(Kernel density estimation-커널 밀도 추정)을 결정하는 방식의 차이에 따라 다른 기법으로 분류됩니다. 각 방법론의 KDE결정 방식은 3.2, 3.3을 참고하시기 바랍니다.
커널 회귀 분석의 추정식은

와 같이 구성됩니다. 즉, m(x)를 구하는 것이 회귀계수를 구하는 것과 같습니다.
3.1 Nadaraya-Wastson 커널 회귀
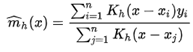
가장 대표적이고 많이 쓰이는 기법으로, K는 커널 기반 함수이고 h는 bandwidth (대역폭) 으로서, h->0 일수록 곡선을 부드럽게 만드는 Smoothing parameter입니다. 커널 회귀는 h의 값에 따라 Local 회귀 계수를 계산하는 구간이 달라집니다. h가 0에 가까울 수록 좁은 구간의 Local 회귀 계수가 산출되고, h가 커질수록 넓은 구간에서 Local 회귀 계수를 계산합니다. h가 0에 가까울수록 부드러운 곡선이 되겠지만, 모델이 Over fitting되지 않게 적절한 h값을 선정하는 것이 중요합니다.

위 그림은 Bandwidth의 값 설정에 따라 회귀곡선이 어떻게 생성되는지 보여주는 예시입니다.
커널 밀도 추정식은

위와 같이 구성되는데, 커널 함수의 내용이 가볍지 않은 만큼 자세한 내용은 다음 시간에 다루도록 하겠습니다.

밀도 함수를 이용한 Y햇, 즉 Y값의 기대값은 위와 같이 유도할 수 있습니다.
3.2 Priestley-chao estimator

3.3 Gasser-Muller estimator

,

위 두 방식은 언뜻 비슷해 보이지만, 추정 시 사용되는 커널 함수와 그 파라미터 범위가 다릅니다. 커널 함수에는 가우스 커널, 시그모이드 커널 등 커널 함수로 사용되는 여러가지 방식들이 있습니다.
4. Addition

위의 사진은 화학물질의 대기 시간에 따른 폭발 시간입니다. 다항 회귀보다 훨씬 Spline된 형태를 보이며, 모델에 잘 적합 된다고 볼 수 있습니다.
5. Restriction
Kernel Regression의 단점으로, 커널의 경계를 찾는데 시간이 많이 소비되고, 대용량 데이터에서 적절하지 않은 것입니다. 이는 알고리즘에 치명적으로 적용되므로, 적절한 h값을 찾아 Local n의 개수를 효율적으로 선정하는 것과, 커널의 경계에 보다 효율적으로 접근하는 방안이 분석가에게 요구됩니다.
NEXT
다음 시간에는 Kernel Regression을 이용하여 회귀 그래프를 작성해 보겠습니다.
'통계학' 카테고리의 다른 글
| [데이터 분석] Weighted Linear Regression- 가중 선형 회귀 (Weighted Least Square) (1) | 2021.12.16 |
|---|---|
| [데이터 분석] Logistic Regression- 로지스틱 회귀 분석 (0) | 2021.12.15 |
| [데이터 분석] Funnel Plot - 깔때기 도표 (0) | 2021.12.05 |
| [회귀 분석] 단순 회귀 모형 추정, 방정식 유도 (1) | 2021.11.28 |
| [통계] 최대 우도 추정(MLE) ,가능도(Likelihood) (0) | 2021.11.27 |




댓글