이번 포스팅에서는 여러가지 주성분 분석 기법들과 그 차이에 대해 알아보겠습니다.
PCA(principle components analysis)
Introduction
여러 개의 변수를 가진 데이터는 고차원 데이터로 불리는데, 이는 저차원 데이터에 비해 계산의 과정이나 효율에 있어서 여러 가지 단점들을 가지게 됩니다. 우리는 주성분 분석을 통해 여러 변수를 한 변수로 축약하거나 차원을 줄임으로써 이 문제를 해결합니다. 주성분의 수를 결정하는 것 또한 하나의 이슈가 될 수 있는데, 이번 포스팅에서는 주성분의 수를 결정하는 세 가지 규칙들을 비교함으로써 그 방법과 차이를 알아 보겠습니다.
세 가지의 기법으로는,
Broken-stick Model
Scree plot
Average of Eigenvalue
를 사용할 것 입니다.
사용할 데이터는 “proc princomp”의 도움말에 나와있는 Crime 데이터 입니다.
이 데이터는 1977 년에 미국 50 개 주에 대한 7 가지 범죄율을 나타내고있습니다.
데이터는 측정치는 10만명당 발생한 범죄건으로서,
| 변수명 | 변수뜻 |
| Muder | 살인 |
| Rape | 강간 |
| Robbery | 강도 |
| Assault | 폭행 |
| Burglary | 빈집털이 |
| Larceny | 도둑질 |
| Auto_theft | 차량절도 |
에 해당하는 건수를 나타내고 있습니다.
Methodology
방법론을 설명함에 앞서서 주성분 분석에 대해 알아보도록 하겠습니다.
주성분 분석이란 차원 축소의 여러 방법 중 한 가지 기법입니다.
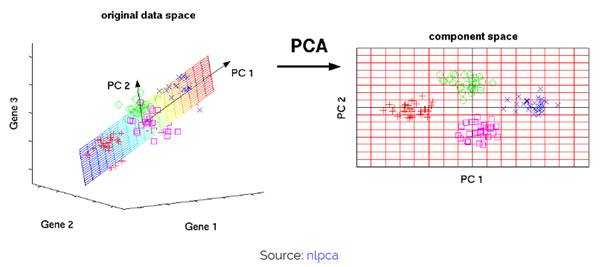
(그림 1)
조금 쉬운 이해를 위해 그림을 가져왔습니다. 말 그대로 고차원에 있는 데이터를 데이터 구조는 그대로 두되, 데이터의 차원을 줄이는 기법을 말합니다. 주성분 분석을 짧게 한 문장으로 표현하자면, 선형 함수를 가지고 데이터가 큰 변동을 가지는 축을 생성하여, 그 축으로 데이터를 정사영 시키는 방법입니다. 여기서 간단하게 짚고 넘어갈 개념은 고유값과 고유벡터, 공분산 행렬입니다. 공분산 행렬의 고유벡터는 데이터가 어떤 방향으로 분산되어 있는지 나타냅니다. 고유 값은 고유벡터에 해당하는 상관 계수에 해당하므로, 우리가 다루는 행렬이 공분산 행렬일 경우 고유 값은 각 축에 대한 공분산 값이 됩니다. 따라서 고유 값이 큰 순서대로 고유 벡터를 정렬하면 결과적으로 중요한 순서대로 주성분을 구하는 것이 됩니다. (고유벡터와 고유값, 공분산 행렬에 대해서는 ‘선형대수학’을 참조하시면 됩니다. 이 장에서는 주성분의 수를 선택하는 것이 주목적이므로 간단히 언급하고 넘어가도록 하겠습니다.)
코드로 구현해보면 먼저 데이터를 생성하고,
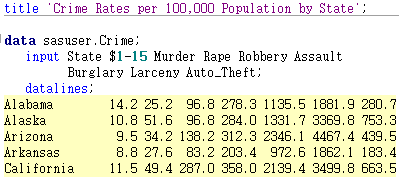
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

(코드1)
(ods graphics on)은 그래프를 생성하는 옵션 문입니다.
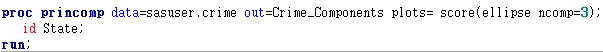
(코드2)-(id state; 문장은 그래프에 주 이름을 함께 출력하기 위한 코드입니다. 일시적인 오류로 빨간색이 되었지만, 문장이 있을 때와 없을 때의 결과값을 비교하시면 될 것입니다.)
여기서 주목해야 할 PROC PRINCOMP 문이 있습니다. 우리는 이 포스팅에서 PROC PRINCOMP를 통한 주성분 분석을 실시할 것입니다. PROC PRINCOMP에는 우선적으로 eigenvalue와 공분산 행렬을 출력하는 기능을 가지고 있습니다. plots= score(ellipse ncomp=3) 문을 보면 주성분 점수로 산점도를 찍고, 타원형 옵션과 성분의 개수를 3개로 지정한 것을 알 수가 있습니다.
상관계수 매트릭스는 각 변수 별로 어떤 상관관계가 있는지를 보여줍니다. 여기서는 특별한 해석 요소가 없기 때문에 생략하겠습니다.
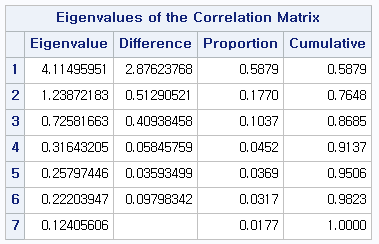
(그림2)
이는 PROC PRINCOMP의 기본으로 출력된 상관행렬의 고유값 측정치 입니다. 위에서 언급했다시피 고유값이 높다는 것은 그 변동이 큰 것임을 알 수 있습니다. 즉, Eigenvalue값이 높을수록 해당 구성요소가 데이터를 잘 설명한다고 볼 수 있습니다. Cumulative 열을 보면 각 고유값들의 합이 얼만큼의 변동을 설명하는가를 볼 수 있습니다. 여기서는 4번째 고유값까지의 누적이 0.9137, 즉 전체 변동의 91퍼센트를 설명하는 것을 알 수가 있습니다.
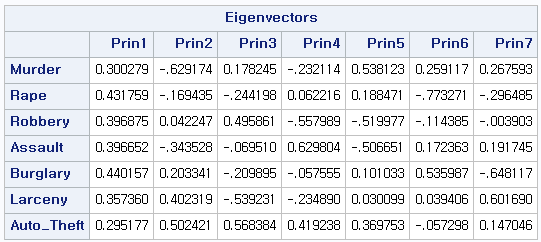
(그림3)
그 다음은 PROC PRINCOMP에 의해 계산된 선형조합의 계수들입니다. 주성분 분석이란 데이터를 포함한 축약된 성분을 만드는데, 여기서는 Prin1…..7을 계산된 주성분이라고 볼 수 있습니다. Prin1은 ‘범죄율’을 나타내는 성분으로서 모든 선형조합이 양의 계수를 가짐을 알 수 있습니다. Prin2는 살인,강간,폭력은 음의 계수, 나머지는 양의 계수임을 보아 Prin2 성분은 재산범죄와 폭력 범죄의 대비율을 보여준다고 해석할 수 있습니다. 구성요소 Prin3~7 에 대한 해석은 분명하지가 않습니다.


(그림5)- 주성분으로 계산된 각 변수들의 선형조합입니다. 주성분의 성질에 따라 다른 계수를 가지며 각 성분이 의미하는 바 또한 다른 의미를 가지고 있습니다.
그러면 다음 단계로는 이 구성요소로 계산된 값들을 어떻게 활용할 지에 대해 알아 보겠습니다.
위에서 실행한 PROC문 (코드2)의 plots= score(ellipse ncomp=3)에 의해
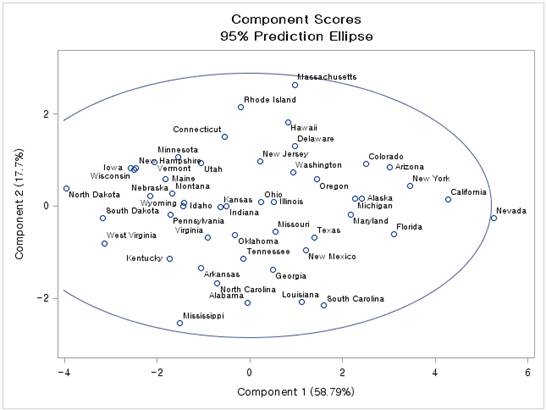
(그림6)
그래프가 생성되었습니다. 위를 해석해보면, Neveda주의 경우 범죄율은 극히 높고, 재산범죄와 폭력범죄의 비율은 비슷한 것으로 볼 수 있습니다. 또한 Mississippi주의 경우는 범죄율도 평균보다 낮지만, 재산범죄에 비해 폭력범죄가 만연히 발생한다는 것을 볼 수가 있습니다.
지금 까지는 주성분 분석의 전반적인 레파토리와 출력값을 보는 방법에 대해 살펴보았습니다.
그러면 조금 더 세부적으로, 주성분의 수를 결정하는 방법에 대해 알아보겠습니다.
Details.
1. scree plot

(코드3)
위의 주성분 코드와 비슷하지만, 조금 더 간단화 하여 실행 시킬 수 있습니다.
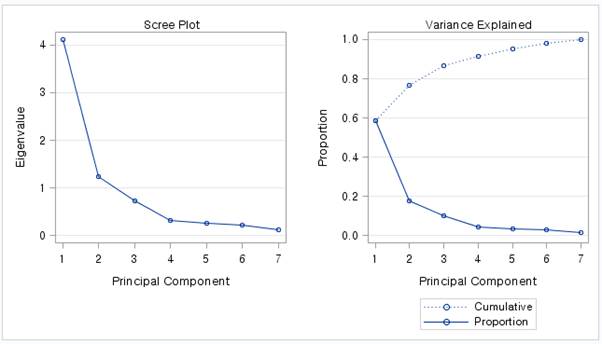
(그림7)
가장 기본적으로 사용되는 (Default)인 Scree plot 방법입니다. 이는 각 변수들의 Eigenvalue 값에 의해 꺾은선 그래프가 그려져 있습니다. 오른쪽을 보시면 eigenvalue의 합들에 대한 비율이 누적그래프로 나와있습니다. 이는 (그림2)를 그래프화 한 것이라고 볼 수 있습니다. 여기서 Scree plot에 의한 주성분 수 선택이란, ‘Ellbow’라는 개념을 확인하여야 합니다. 팔꿈치라고 해석되는 이 개념은Scree plot 에서 ‘꺾인점’을 찾는 것이라고 생각하시면 됩니다. 위 데이터에서는 주성분 2와 주성분 4에서 그래프가 꺾인다는 것을 볼 수 있습니다. 즉, 주성분 수를 2개로 하거나 4개로 하는 것이 효율적인 것이라고 볼 수 있습니다. 실제로 (그림2)의 누적값을 확인 했을 때도, 주성분이 2개 일 때는 총 변동의 76퍼센트를, 4개 일 때는 91퍼센트를 설명하는 것을 알 수가 있습니다.
2. Broken Stick Model
Broken Stick의 모델은 새로운 예상비율 그래프를 만들어 그 예상 비율보다 높은 성분만을 주성분으로 채택하는 방법입니다. ‘부러진 막대’라는 개념은 ‘예상비율 그래프를 만드는 방법론에 의해서 지어진 이름입니다.
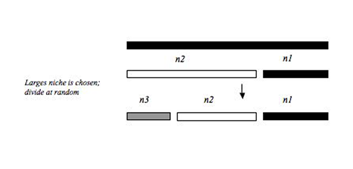
(그림8)-Niche apportioment model-(broken stick모델로부터 확장된, 유사한 모형, broken stick model의 그림을 찾을 수가 없어서 가져왔다.)
위 막대 나눔 같이 총 변동을 1이라고 두면 한 구성요소가 추가 될 때 마다 1, 1/2, 1/3 …씩 설명한다고 판단합니다. 그 결과의 합들로 예상비율 그래프를 작성합니다. 위의 데이터 같은 경우는 고유값이 7개이므로, 위 데이터의 예상비율 그래프의 점은 broken stick model의 (1/p)Σ(1/i)를 따른다..
E1 = (1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7) / 7 = 0.37, (주성분을 한 개로 보았을 때)
E2 = (1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7) / 7 = 0.228, (주성분을 두 개로 보았을 때)
E3 = (1/3 + 1/4 + 1/5 + 1/6 + 1/7) / 7 = 0.156. (주성분을 세 개로 보았을 때)
Etc…
예상비율의 계산 값은 위와 같습니다.
코드를 사용하여 출력해 봅시다.

(코드4)
여기서 주의 할 점은 Broken Stick 의 예상 비율 값과 기존그관찰 값을 비교하려면 ‘PROC IML’문을 쓰셔야 한다는 것입니다. IML에 대한 자세한 사항은 생략하고 간단히 코드만 참조하시기 바랍니다.
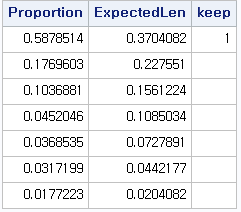
실제 SAS의 출력 값 또한 주성분으로 채택된 주성분은 한 가지 인 것을 알 수가 있습니다.
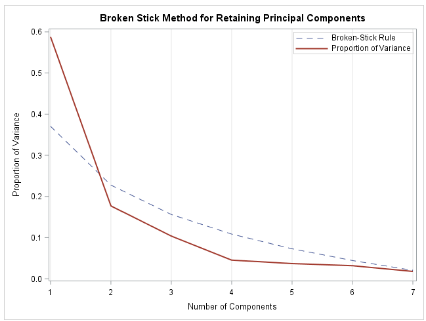
(그림9) 예상비율 그래프와 관찰된 eigenvalue의 proportion 그래프의 비교
Broken stick model은 예상 비율 값보다 관찰 비율 값이 높이 측정된 eigenvalue 만을 주성분으로 채택하는 것 이 관건입니다. 위의 그래프는 첫 번 째 주성분에서만 예상비율 그래프보다 관찰 값이 높으므로, 첫 번 째 요소만 주성분으로 채택합니다.

(코드5) 이는 (그림 9)의 그래프를 출력하는 SAS 코드입니다.
3. Average of Eigenvalue
평균 고유값 방법은 쉽게 말해서 평균 eigenvalue 값보다 높은 eigenvalue의 주성분을 유지하는 방법입니다.

위의 코드는 평균보다 proportion이 높은 것을 유지합니다. 밑의 코드는 Jolliffe (1972)이 제안한 평균의 0.7배보다 높은 값을 가지는 성분을 유지하는 코드입니다. 조금 더 완화된 코드라고 볼 수 있습니다.
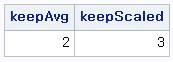
출력값은 매우 간단합니다. 평균보다 큰 고유값은 두 개, 평균의 0.7배보다 높은 고유값은 주성분을 세 개로 유지합니다.
Summary
우리는 오늘 여러가지 방법을 통해 주성분의 수를 결정하는 법을 알아보았습니다. 각자의 방법론에 따라 유지하는 주성분 수가 다르다는 것 또한 확인하였습니다. (scree plot-2 또는 4개 broken stick-1개 average of eigenvalue – 2 또는 3개) 위의 세가지 방법들 중 무엇이 가장 좋고 옳은지는 말 할 수 없습니다. 다만 위의 방법론들은 가이드 라인을 제시할 뿐, 어떤 기법을 선택하느냐는 전적으로 통계 전문가의 책임입니다.
'통계학' 카테고리의 다른 글
| [데이터 분석] Logistic Regression- 로지스틱 회귀 분석 (0) | 2021.12.15 |
|---|---|
| [데이터 분석] Kernel Regression- 커널 회귀 (1) | 2021.12.06 |
| [데이터 분석] Funnel Plot - 깔때기 도표 (0) | 2021.12.05 |
| [회귀 분석] 단순 회귀 모형 추정, 방정식 유도 (1) | 2021.11.28 |
| [통계] 최대 우도 추정(MLE) ,가능도(Likelihood) (0) | 2021.11.27 |




댓글