부제: 가능도와 최대 가능도 추정
안녕하세요 파키노랩입니다.
Josh Starmer의 유투브 자료는 참고를 위해 게시글 하단에 첨부하겠습니다.
1. Introduction
통계학에서 많이 사용되는 MLE 개념은 최대의 가능도(우도)를 추정하는 방법입니다. 가능도라는 개념도 참 애매모호합니다. 뭐가 가능하길래 확률과 다른걸까요? 가능도 또한 모수를 추정하는 방법중 하나입니다. Likelihood와 MLE에 대해 알아보겠습니다.
2. Likelihood
가능도란 " 관측값 A가 관측되었을때 , 어떠한 분포 B에 해당할 확률" 입니다. 즉 관측된 A의 모집단 분포는 어떤 분포에 해당할까~? 라는 질문에서 시작되었습니다. 예를 들어 어떤 물체 A의 무게가 20g이라고 하면, 이 물체의 모집단 분포는 어디에 가까울까요? 평균이 10g인 집단에 가까울까요, 아니면 평균이 20g인 집단에 가까울까요. 당연히 평균이 20g인 집단에 속할 "확률"이 높다고 판단됩니다. 여기서의 확률이 가능도가 되는겁니다. 이를 통해 우리는 모집단을 통계적으로 추정할 수 있습니다.
그림을 통해 이해해보죠.

어떤 쥐의 무게가 34g(빨간점)로 측정되었습니다. 그러면 모든 쥐의 집단(모집단)이 평균 32, 표준 편차 2.5인 분포를 따를 확률은 0.11쯤 됩니다. 여기서 말하는 0.11이 가능도가 되는거죠. 조금 이해가 되시나요?
그러면 최대 가능도라는 건 무엇을 의미할까요? 위에 말했다시피 관측값 A의 모집단 분포는 A 측정값 그 자체를 평균으로 가질 때 가장 큰 가능도를 갖겠죠.

반면에 평균 32가 아닌 평균 34, 표준편차 2.5인 분포가 모집단일 "확률"(가능도)은 0.21입니다. 이 0.21값이 최대 가능도가 되는 것입니다. 이해가 되시나요? 이 가능도가 최대값일 때를 추정하는 함수가, "MLE, 최대가능도 함수" 가 되겠습니다.
3. Maximum Likelihood Estimation
그림과 예시를 통해 최대 가능도 추정을 이해해보았습니다. 이제 수식적으로 접근해보죠.

가능도 함수
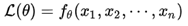
최대 가능도 방법
가능도와 최대 가능도 함수 수식입니다. 가능도라는 것이 어떤 특정한 X값에 대한 분포를 추정하는 것이라면, 최대 가능도 함수란 확률질량함수 F로부터 얻은 각각의 x값들에 의한 추정값입니다.
이 때, 확률 밀도 함수로부터 출력된 X1,X2,,,Xn이 각각 독립적이라면, 가능도를 다음과 같이 나타낼 수 있습니다.

여기서 가능도를 최대로 만드는\theta 는
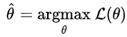
와 같이 정리됩니다. 핵심은 theta를 찾아내는 것이므로 theta 추정 값을 사용하는 것입니다.
최대가능도 추정은 어떤 과정을 말하는 걸까요?

모집단의 분포가 정규분포이고, 왼쪽에 치우쳐져 있다고 가정합시다. 그러면, 우측에 해당하는 관측치들이 갖는 가능도는 아주 낮게 됩니다. 위의 분포가 자신의 모집단일 확률이 낮게 추정되는 것이죠. 아까 말했다시피, 자기 자신의 값을 평균으로 갖는 분포에 대한 가능도가 가장 높을 것입니다.
그러면 관측된 값들을 가장 잘 나타내는 분포를 찾아내는 과정이 최대 가능도 추정이라고 할 수 있겠습니다. 그림으로 표현해 볼까요?
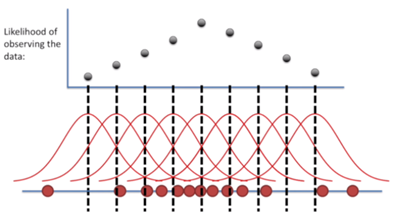
관측 값들을 잘 나타내는 모집단 분포를 여러 개 고민해보았고, 그 분포들의 가능도를 가시화했습니다. 예상한대로, 관측값들과 가장 유사한 분포가 가장 높은 가능도를 갖게 됩니다. 바로 이 일련의 과정을 최대가능도추정 이라고 일컫습니다.
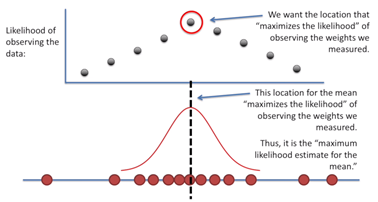
바로 저 가운데 있는 검은색 점이 나타내는 Y값이 추정된 가능도 중 최대의 가능도 값입니다.
4. Conclusion
가능도라는건 아무리 전공자라도 설명하기 어려운 개념 같습니다. 다행히 이번에 참고한 자료가 좋아서 저도 설명하면서 이해하기 수월하겠다는 느낌을 받았습니다. 도움이 많이 되셨기를 바라며, 원하는 개념이나 기법이 있으면 댓글로 남겨주세요!
https://www.youtube.com/watch?v=XepXtl9YKwc
'통계학' 카테고리의 다른 글
| [데이터 분석] Logistic Regression- 로지스틱 회귀 분석 (0) | 2021.12.15 |
|---|---|
| [데이터 분석] Kernel Regression- 커널 회귀 (1) | 2021.12.06 |
| [데이터 분석] Funnel Plot - 깔때기 도표 (0) | 2021.12.05 |
| [회귀 분석] 단순 회귀 모형 추정, 방정식 유도 (1) | 2021.11.28 |
| [PCA] 주성분 수를 결정하는 여러가지 PCA 방법론 (SAS) (0) | 2021.11.27 |




댓글